[This is just one of many articles in the author’s Astronomy Digest.]
Our eyes are a wonderful creation − capable of seeing over a very wide range of brightness levels from a sunny beach to a dark location from which to observe the heavens. The first part of this article looks at how our eyes adapt to the dark and so allow us to see faint stars and even four galaxies − M31, M33 and the two Magellanic Clouds − with our unaided eyes.
As we step from a bright room into the dark outside the first, and virtually instantaneous, adaptation to the dark is that the pupils of our eyes dilate from perhaps 2 mm up to 5 to 7 mm in diameter. As indicated in the addendum at the end of this article the size of the dilated pupil depends quite strongly on age falling from ~7 mm at age 25 down to ~5 mm at age 70. This represents a factor of 2 in area so that, other things being equal, a young person would be able to see stars up to ~0.75 magnitudes fainter than an elderly person. [Mdiff = 2.5 log10(2)] The magnitude gain may not be quite as much as this as, when the pupil is wide open, aberrations in the eye’s optics may increase the size of stellar images on the retina somewhat making them slightly harder to detect.
Using direct vision, we observe the light falling on the fovea in the central part of the retina. This small area is densely packed with the cones that give us our colour vision. It contains few of the rods that register only brightness. In the dark, the sensitivity of the cones increases quite rapidly so enabling us to see fainter stars. They reach their full sensitivity after 7 to 10 minutes.
Away from the fovea, the cones are sparse and our vision depends on the rods. They too will increase in sensitivity but the time scale is longer, taking 30 to 50 minutes to reach their full sensitivity − which is considerably greater than that of the cones. So we will see fainter objects when using averted vision; that is directing ones eyes slightly away from the object that we wish to view but still concentrating on the object of interest. This takes some practice. The sensitivity of the retina is not uniform away from the fovea, being most sensitive in the part of the retina nearest the nose, so that one should scan around the object of interest until the object is best seen.
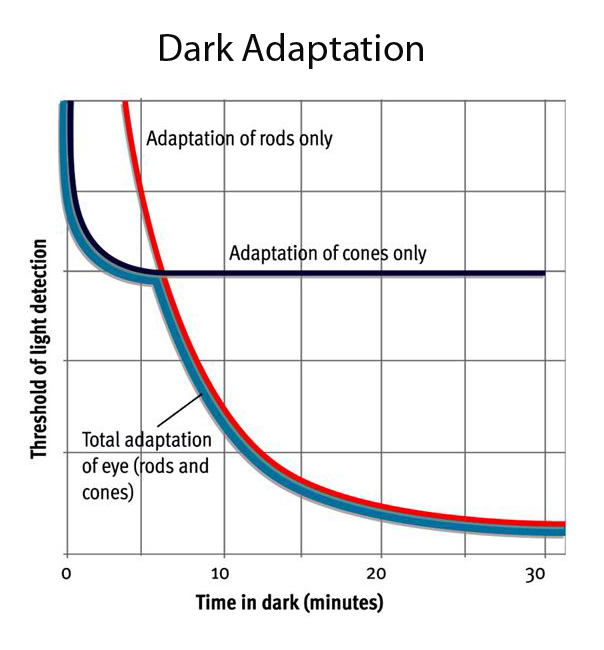
Dark Adaptation of the Cones and Rods
Some observers report that their sensitivity is increased by 20-40 times corresponding to a magnitude increase of 3 to 4 magnitudes.
The Blinking Nebula, NGC 6826, that lies in Cygnus and is almost overhead in midsummer, is an object that dramatically demonstrates averted vision. When viewing this using a small telescope and using direct vision to observe this blue-green planetary nebula, one will only see the dim central star. Using averted vision and looking slightly to one side or the other, the faint nebula around the star appears. Switching quickly from straight to averted vision and back, the nebula appears to blink on and off − hence its name.
Hubble Telescope Image of the Blinking Nebula
NELM − Naked Eye Limiting Magnitude
The limiting magnitude, NELM, is a reference to the faintest stars that can be seen with the unaided eye near the zenith. NELM is most often used as an overall indicator of sky brightness, in that light polluted and humid areas generally have brighter limiting magnitudes than remote desert or high altitude areas. The limiting magnitude will depend on the observer, and will increase with the eye’s dark adaptation. Under a relatively clear sky, the limiting visibility will be about 6th magnitude. NELM is generally regarded as the maximum magnitude that can be detected using averted vision. As this is very observer specific, I am not too keen on this definition and, at the end of this article, am proposing an alternative.
As the light from very faint stars will cause few photons to enter the eye, the fact that randomness in their numbers entering the eye during a period of about 1/30th second − which is about the ‘integration’ time of the eye − means that at the limit, stars will only be visible for brief moments of the time and star will appear to ‘blink’ in at out. If seen several times over a short period of time, observers can claim to have seen the star. This is how some observers can observe stars down to 8th magnitude on dark, moonless nights!
I have been lucky enough to observe the night sky from some of the darkest locations on Earth but there is no doubt that the ‘sky’ that excited me most, and where my NELM was greatest, was when I was at the site of the Sutherland Observatory in South Africa at a height of 1,800 m. [Height does help, but if at very high altitudes the amount of oxygen reaching the brain is reduced and our eyes become less efficient. It is reckoned that ~2,400 m is about optimum. From a height of 2,800 m on the flanks of Mauna Kea, I have observed the dark part of the Moon lit by earthshine when the sunlit part had set behind mountains. It appeared as bright to me as a bright moon appears from the UK at sea level.
One might expect that the sky might appear blacker from very dark sites. Perhaps surprisingly, it doesn’t and actually gets brighter as we become dark adapted. It is a dark grey colour which can vary in brightness somewhat. We are seeing light that is scattered from stars and the Milky Way, sunlight scattered from dust in the plane of the solar system (the Zodiacal Light) and ‘Airglow’. This latter cause is more apparent at lower elevations and a major part comes from emission of the O III line in the green produce by oxygen that has been excited by ultraviolet emission from the Sun during the previous day. I have only observed and photographed this once, from the Kerry Dark Sky Reserve in Ireland, and discussed it in the essay ‘Imaging the Milky Way from the Kerry Dark Sky Reserve’. The airglow affects even the highest observatories, which is one reason why the Hubble Space Telescope, though small, performs so well compared to, far larger, Earth bound telescopes.
Sky Quality Meters.
The company Unihedron manufacture meters which measure the brightness of the sky in magnitudes per square arcsecond. This is a logarithmic measurement so large changes in sky brightness correspond to relatively small numerical changes. The numerical output ranges from 16 under moonlight to ~21 under the darkest skies. Their use is very simple: one simply points the lens to the zenith and presses the start button. Under urban skies a reading will be made almost immediately. From the very darkest sights, it may take up to a minute to make a measurement during which time it clicks quietly.

Unihedron SQM-L Meter
The value of NELM can then be found using a calculator that can be accessed from the web:
As an example, from my home location 1 mile from the centre of a medium sized town on a transparent sky with no moonlight, I have obtained an SQM reading of 20 which corresponds to NELM of 5.5 magnitudes. This is actually quite impressive and, I suspect, somewhat better than in the past − perhaps the new LED street lights are having a beneficial effect.
DVLM – Direct Vision Limiting Magnitude
I would much prefer a definition of limiting magnitude that does not require the use of averted vision so have come up with the name DVLM for Direct Vision Limiting Magnitude − which will, of course, be less that NELM from any given site and observing condition. As the cones which are used for direct vision reach their maximum sensitivity after, say, 10 minutes one would not have to wait so long to make an observation. I suspect that results from a wide variety of observers would be far more consistent than measurements of NELM. By adding to the DVLM a suitable amount, which might well be in the region of 1.5-2 magnitudes, one could derive a value of NELM which would agree with the values obtained using the Unihedron SQM-L Meter. I hope to explore this thought further to find, using a number of observers, the appropriate correction to give NELM. As the DVLM will depend on age due to the fact that as we age our pupils dilate less, the correction should, I think, include an age term. From my own initial observations I have come up with the formula:
NELM = DVLM + 1.5 + ((Age-20) x 0.01)
This latter term would give an additional contribution of up to 0.5 magnitudes and could be replaced by a value:
Age Magnitude correction
Up to 30 0.0
30 to 40 0.1
40 to 50 0.2
50 to 60 0.3
60 to 70 0.4
70+ 0.5
So as an example, on the night when the SQ meter gave a value of 5.5 magnitudes for NELM my DVLM was 3.5 magnitudes so:
NELM = 3.5 + 1.5 + ((70 -20) x 0.01) = 3.5 + 1.5 + 0.5 = 5.5
Addendum: Dark adapted Pupil Diameters
In 2011 a study was published of 263 individuals aged 18 to 80. The mean measured dark adapted pupil diameters as a function of age is given below.
Age Diameter (mm)
20-29 7.33
30-39 6.6
40-49 6.15
50-59 5.77
60-69 5.58
70-79 5.17
[This latter group ranged from 4.6 to 6 mm.]
